McElreath Chapter 4

Working through a few practice problems on Linear Regression.
statistical-rethinking
bayesian
Published

April 10, 2022

Code 
import arviz as az
import pandas as pd
import numpy as np
import pymc3 as pm

from matplotlib import pylab as plt
from scipy import stats

from patsy import dmatrix

az.style.use("arviz-darkgrid")
az.rcParams["stats.hdi_prob"] = 0.89

4M1

For the model definition below, simulate observed \(y\) values from the prior (not the posterior).

\[y \sim \text{Normal}(\mu, \sigma) \] \[\mu \sim \text{Normal}(0, 10) \] \[\sigma \sim \text{Exponential}(1) \]

n_samples = 1000
sample_mu = stats.norm.rvs( loc=0, scale=10, size=n_samples )
sample_std = stats.expon.rvs( scale=1 , size=n_samples )
sample_y = stats.norm.rvs( loc=sample_mu, scale=sample_std, size=n_samples )
az.plot_kde(sample_y)
plt.title('Distribution of Prior Predictive values')
Text(0.5, 1.0, 'Distribution of Prior Predictive values')

plt.hist(sample_y)
(array([ 10.,  35., 116., 202., 232., 218., 118.,  47.,  17.,   5.]),
 array([-30.14262363, -23.65619686, -17.1697701 , -10.68334333,
         -4.19691657,   2.2895102 ,   8.77593697,  15.26236373,
         21.7487905 ,  28.23521727,  34.72164403]),
 <a list of 10 Patch objects>)

4M4

A sample of students is measured for height each year for 3 years. After the third year, you want to fit a linear regression predicting height using year as a predictor. Write down the mathematical model definition for this regression, using any variable names and priors you choose. Be prepared to defend your choice of priors.

Let \(h_{ij}\) be the height of the \(i\)-th student in year \(j\) (where \(j \in \{1,2,3\}\)).

\[h_{ij} \sim N(\mu_{ij},\sigma)\] \[\mu_{ij} = \alpha + \beta(x_{ij}-\bar{x})\] \[\alpha \sim N(100,10)\] \[\beta \sim \text{Normal}(0,10)\] \[\sigma \sim \text{Exponential}(1)\]

  • Let \(x_{ij}\) be the year corresponding to student \(i\) for year \(j\) in the dataset.
    • In particular, \(x_{i1}=1, x_{i2}=2\) and \(x_{i3}=3\).
  • Let \(\bar{x}\) be the average year in the dataset.
    • As each student was measured for height each year, \(\bar{x} = \frac{1+2+3}{3}=2\).
  • The mean height of the students is taking to be 100 cm.
  • The Exponential is used as the prior distribution for \(\sigma\) (the standard deviation) to constrain it to be positive.

Next, let’s simulate a dataset consisting of 40 children:

n_samples = 40
sample_alpha = stats.norm.rvs( loc=100, scale=10, size=n_samples )
sample_beta = stats.norm.rvs( loc=0, scale=10, size=n_samples )
sample_std = stats.expon.rvs( scale=1 , size=n_samples )

years = np.array([1,2,3])
xbar = np.mean( years )

# sample_y = stats.norm.rvs( loc=sample_mu, scale=sample_std, size=n_samples )
# Each row is a student, column 1 is for year-1, column 2 is for year-2 and
# column 3 is for year-3
sample_mu = ( sample_alpha.reshape(n_samples, 1) + 
             sample_beta.reshape(n_samples, 1) * (years - xbar).reshape(1, 3) )
# Each row is a student, column 1 is for year-1, column 2 is for year-2 and
# column 3 is for year-3
sample_height = np.zeros((n_samples, 3))
for i in range(n_samples):
  for j in years:
    mu_ij = sample_alpha[i] + sample_beta[i]*(j - xbar)
    sample_height[i, j-1] = stats.norm.rvs( mu_ij , sample_std[i] )
for i in range(n_samples):
  plt.plot( years , sample_height[i] , color='blue' )
plt.xticks( years )
plt.xlabel( 'year' )
plt.ylabel( 'height (cm)' )
Text(0, 0.5, 'height (cm)')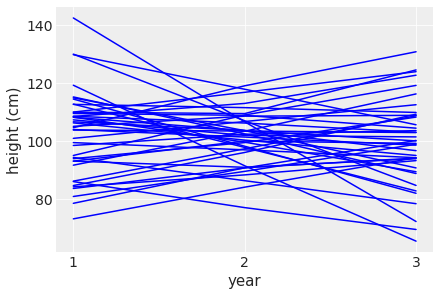

Each line tracks the simulated height of each student across the 3 years. Clearly there are some nonsensical relationships here where the height for some students actually goes down across the years.

4M5

Now suppose I remind you that every student got taller each year. Does this information lead you to change your choice of priors? How?

Yes, we can impose a Log-Normal prior on the slope so that it is constrained to be positive. Per [1], if \(Z \sim \text{Normal}(0,1)\) and if \(\mu\) and \(\sigma > 0\) are two real numbers then \(\beta = e^{\mu + \sigma Z}\) is log-normally distributed with parameters \(\mu\) and \(\sigma\). Also \(E[\beta] = e^{\mu + \frac{1}{2}\sigma^{2}}\). * So if \(\mu=1\) and \(\sigma=0.1\) then \(E[\beta] \approx 2.73 \text{cm/year}\)

n_samples = 40
sample_alpha = stats.norm.rvs( loc=100, scale=10, size=n_samples )
sample_beta = np.random.lognormal( mean=1, sigma=0.1, size=n_samples)
sample_std = stats.expon.rvs( scale=1 , size=n_samples )

years = np.array([1,2,3])
xbar = np.mean( years )

sample_height = np.zeros((n_samples, 3))
for i in range(n_samples):
  for j in years:
    mu_ij = sample_alpha[i] + sample_beta[i]*(j - xbar)
    sample_height[i, j-1] = stats.norm.rvs( mu_ij , sample_std[i] )
for i in range(n_samples):
  plt.plot( years , sample_height[i] , color='blue' )
plt.xticks( years )
plt.xlabel( 'year' )
plt.ylabel( 'height (cm)' )
Text(0, 0.5, 'height (cm)')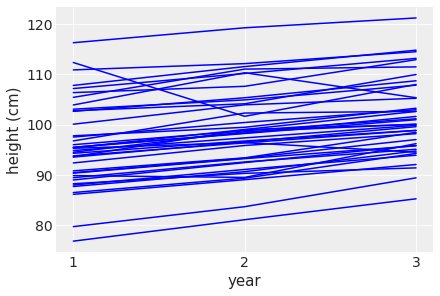

This looks much better with height increasing across the years. However there are still some weird observations where the height zig-zags.

4M6

Now suppose I tell you that the variance among heights for students of the same age is never more than 64cm. How does this lead you to revise your priors?

This would lead me to set \(\sigma \sim \text{Uniform}(0,\sqrt{64})\)

4M7

Refit model m4.3 from the chapter, but omit the mean weight xbar this time. Compare the new model’s posterior to that of the original model. In particular, look at the covariance among the parameters. What is different? Then compare the posterior predictions of both models.

height weight age male
0 151.765 47.825606 63.0 1
1 139.700 36.485807 63.0 0
2 136.525 31.864838 65.0 0
3 156.845 53.041914 41.0 1
4 145.415 41.276872 51.0 0 
xbar = d2.weight.mean()

with pm.Model() as m4_3:
    a = pm.Normal("a", mu=178, sd=20)
    b = pm.Lognormal("b", mu=0, sd=1)
    sigma = pm.Uniform("sigma", 0, 50)
    mu = a + b * (d2.weight - xbar)
    height = pm.Normal("height", mu=mu, sd=sigma, observed=d2.height)
    trace_4_3 = pm.sample(1000, tune=1000, return_inferencedata=False)

with pm.Model() as m4M7:
  alpha = pm.Normal( 'alpha', mu=178, sd=20 )
  beta = pm.Lognormal( 'beta', mu=0, sd=1 )
  sigma = pm.Uniform( 'sigma' , lower=0, upper=50 )
  mu = alpha + beta*d2.weight
  height = pm.Normal( 'height' , mu=mu, sd=sigma, observed=d2.height )
  trace_4M7 = pm.sample(1000, tune=1000, return_inferencedata=False)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Sequential sampling (2 chains in 1 job)
NUTS: [sigma, b, a]
Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 19 seconds.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Sequential sampling (2 chains in 1 job)
NUTS: [sigma, beta, alpha]
Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 27 seconds.
The acceptance probability does not match the target. It is 0.8897350788344733, but should be close to 0.8. Try to increase the number of tuning steps.
100.00% [2000/2000 00:10<00:00 Sampling chain 0, 0 divergences]
100.00% [2000/2000 00:08<00:00 Sampling chain 1, 0 divergences]
100.00% [2000/2000 00:13<00:00 Sampling chain 0, 0 divergences]
100.00% [2000/2000 00:13<00:00 Sampling chain 1, 0 divergences] 
az.summary(trace_4M7, kind="stats")
Got error No model on context stack. trying to find log_likelihood in translation.
/usr/local/lib/python3.7/dist-packages/arviz/data/io_pymc3_3x.py:102: FutureWarning: Using `from_pymc3` without the model will be deprecated in a future release. Not using the model will return less accurate and less useful results. Make sure you use the model argument or call from_pymc3 within a model context.
  FutureWarning,
mean sd hdi_5.5% hdi_94.5%
alpha 114.491 1.858 111.612 117.473
beta 0.892 0.041 0.826 0.955
sigma 5.093 0.202 4.750 5.383 
az.summary(trace_4_3, kind="stats")
Got error No model on context stack. trying to find log_likelihood in translation.
/usr/local/lib/python3.7/dist-packages/arviz/data/io_pymc3_3x.py:102: FutureWarning: Using `from_pymc3` without the model will be deprecated in a future release. Not using the model will return less accurate and less useful results. Make sure you use the model argument or call from_pymc3 within a model context.
  FutureWarning,
mean sd hdi_5.5% hdi_94.5%
a 154.604 0.281 154.128 155.004
b 0.903 0.043 0.839 0.975
sigma 5.104 0.202 4.774 5.416

Model 4_3 intercept (a) is larger than in M47 (alpha) but the slope is roughly the same.

Plot the posterior inference against the data

Superimpose the posterior mean values over the height and weight data

plt.scatter(d2['weight'], d2['height'])
plt.plot(d2['weight'], ( trace_4M7['alpha'].mean() + 
                        trace_4M7['beta'].mean()*d2['weight'] ),
         color='orange' )
plt.xlabel(d2.columns[1])
plt.ylabel(d2.columns[0])
Text(0, 0.5, 'height')

Add the uncertainty around the mean

First add the uncertainty around the average height.

trace_iq = trace_4M7 #trace in question
posterior_samples = np.random.randint(len(trace_iq), size=10000)
weight_seq = np.arange(0, 71)
cred_intervals = np.array(
    [ az.hdi( trace_iq['alpha'][posterior_samples] + 
             trace_iq['beta'][posterior_samples]*wt ) for wt in weight_seq ]
)
cred_intervals.shape
(71, 2)
plt.scatter(d2['weight'], d2['height'])
plt.plot(weight_seq, ( trace_4M7['alpha'].mean() + 
                        trace_4M7['beta'].mean()*weight_seq ),
         color='orange' )
plt.fill_between(
    weight_seq, cred_intervals[:, 0], cred_intervals[:, 1], alpha=0.4, 
    label=r"Uncertainty in $\mu$",
)
plt.xlabel(d2.columns[1])
plt.ylabel(d2.columns[0])
plt.axvline(np.mean(d2.weight), ls="--", c="r", label="Mean weight")
plt.legend()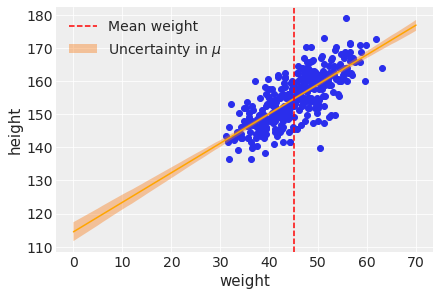
<matplotlib.legend.Legend>

Add the prediction intervals

Next add the uncertainty around the actual heights making use of the standard deviation.

trace_iq['alpha'][posterior_samples].shape
(10000,)
# define a function to compute mu for all posterior samples at given value of 
# weight
def compute_mu(w):
    return ( trace_iq['alpha'][posterior_samples] + 
            trace_iq['beta'][posterior_samples] * w )

pi_67 = np.array(
    [
        az.hdi(np.random.normal(loc=compute_mu(x), 
                                scale=trace_iq['sigma'][posterior_samples]), 
                                hdi_prob=0.67)
        for x in weight_seq
    ]
)

pi_89 = np.array(
    [
        az.hdi(np.random.normal(loc=compute_mu(x), 
                                scale=trace_iq['sigma'][posterior_samples]))
        for x in weight_seq
    ]
)

pi_97 = np.array(
    [
        az.hdi(np.random.normal(loc=compute_mu(x), 
                                scale=trace_iq['sigma'][posterior_samples]), 
                                hdi_prob=0.97)
        for x in weight_seq
    ]
)
plt.scatter(d2['weight'], d2['height'])
plt.plot(weight_seq, ( trace_4M7['alpha'].mean() + 
                        trace_4M7['beta'].mean()*weight_seq ),
         color='black' )
plt.fill_between(
    weight_seq, cred_intervals[:, 0], cred_intervals[:, 1], alpha=0.2, 
    label=r"Uncertainty in $\mu$",
)
plt.fill_between(
    weight_seq, pi_67[:, 0], pi_67[:, 1], 
    alpha=0.2, color='blue' 
)
plt.fill_between(
    weight_seq, pi_89[:, 0], pi_89[:, 1], 
    alpha=0.1, color='blue' 
)
plt.fill_between(
    weight_seq, pi_97[:, 0], pi_97[:, 1], 
    alpha=0.05, color='blue' 
)
plt.xlabel(d2.columns[1])
plt.ylabel(d2.columns[0])
plt.axvline(np.mean(d2.weight), ls="--", c="r", label="Mean weight")
plt.xlim(d2.weight.min(), d2.weight.max());
plt.legend()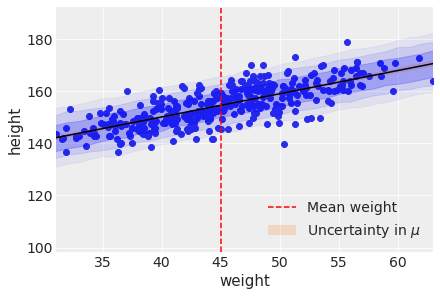
<matplotlib.legend.Legend>

Another way to generate the same plot.

# Given that we have 2,000 samples let's use 200 for plotting 
# (or we can use all of them too if desired)
trace_iq_thinned = trace_iq[::10]
mu_pred = np.zeros((len(weight_seq), len(trace_iq_thinned) * trace_iq.nchains))
for i, w in enumerate(weight_seq):
    mu_pred[i] = ( trace_iq_thinned["alpha"] + 
                  trace_iq_thinned["beta"] * w )
trace_iq_thinned, mu_pred.shape
(<MultiTrace: 2 chains, 100 iterations, 5 variables>, (71, 200))
mu_mean = mu_pred.mean(1) 
mu_hdi = az.hdi(mu_pred.T)
mu_mean.shape, mu_hdi.shape
/usr/local/lib/python3.7/dist-packages/ipykernel_launcher.py:2: FutureWarning: hdi currently interprets 2d data as (draw, shape) but this will change in a future release to (chain, draw) for coherence with other functions
  
((71,), (71, 2))

Generate heights from the posterior manually.

post_samples = []
for _ in range(10000):  # number of samples from the posterior
    i = np.random.randint(len(trace_iq))
    mu_pr = trace_iq['alpha'][i] + trace_iq['beta'][i] * weight_seq
    sigma_pred = trace_iq['sigma'][i]
    post_samples.append(np.random.normal(mu_pr, sigma_pred))
ax=az.plot_hdi(weight_seq, mu_pred.T)
az.plot_hdi(weight_seq, np.array(post_samples), ax=ax, hdi_prob=0.67)
az.plot_hdi(weight_seq, np.array(post_samples), ax=ax, hdi_prob=0.89)
az.plot_hdi(weight_seq, np.array(post_samples), ax=ax, hdi_prob=0.97)
plt.scatter(d2.weight, d2.height)
plt.plot(weight_seq, mu_mean, "k")
plt.axvline(np.mean(d2.weight), ls="--", c="r", label="Mean weight")
plt.xlabel("weight")
plt.ylabel("height")
plt.xlim(d2.weight.min(), d2.weight.max());
/usr/local/lib/python3.7/dist-packages/arviz/plots/hdiplot.py:157: FutureWarning: hdi currently interprets 2d data as (draw, shape) but this will change in a future release to (chain, draw) for coherence with other functions
  hdi_data = hdi(y, hdi_prob=hdi_prob, circular=circular, multimodal=False, **hdi_kwargs)
/usr/local/lib/python3.7/dist-packages/arviz/plots/hdiplot.py:157: FutureWarning: hdi currently interprets 2d data as (draw, shape) but this will change in a future release to (chain, draw) for coherence with other functions
  hdi_data = hdi(y, hdi_prob=hdi_prob, circular=circular, multimodal=False, **hdi_kwargs)
/usr/local/lib/python3.7/dist-packages/arviz/plots/hdiplot.py:157: FutureWarning: hdi currently interprets 2d data as (draw, shape) but this will change in a future release to (chain, draw) for coherence with other functions
  hdi_data = hdi(y, hdi_prob=hdi_prob, circular=circular, multimodal=False, **hdi_kwargs)
/usr/local/lib/python3.7/dist-packages/arviz/plots/hdiplot.py:157: FutureWarning: hdi currently interprets 2d data as (draw, shape) but this will change in a future release to (chain, draw) for coherence with other functions
  hdi_data = hdi(y, hdi_prob=hdi_prob, circular=circular, multimodal=False, **hdi_kwargs)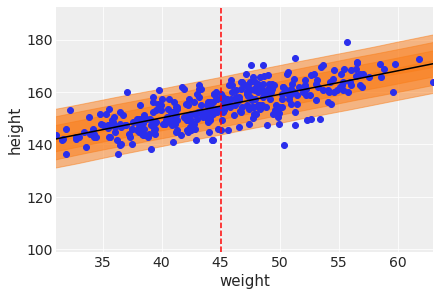

trace_4M7_df = pm.trace_to_dataframe( trace_4M7 )
trace_4M7_df.cov().round(3)
alpha beta sigma
alpha 3.452 -0.076 -0.026
beta -0.076 0.002 0.001
sigma -0.026 0.001 0.041

There doesn’t seem to be much of a covariance between the parameters. This is similar to what we saw in m_4_3 (shown below).

pm.trace_to_dataframe( trace_4_3 ).cov().round(3)
a b sigma
a 0.079 -0.000 -0.000
b -0.000 0.002 0.000
sigma -0.000 0.000 0.041

Next let’s examine the correlations.

trace_4M7_df.corr().round(3)
alpha beta sigma
alpha 1.00 -0.99 -0.07
beta -0.99 1.00 0.07
sigma -0.07 0.07 1.00

Intercept (alpha) and slope (beta) are negatively correlated unlike model m_4_3.

pm.trace_to_dataframe( trace_4_3 ).corr().round(3)
a b sigma
a 1.000 -0.041 -0.000
b -0.041 1.000 0.051
sigma -0.000 0.051 1.000

4M8

In the chapter, we used 15 knots with the cherry blossom spline. Increase the number of knots and observe what happens to the resulting spline. Then adjust also the width of the prior on the weights – change the standard deviation of the prior and watch what happens. What do you think the combination of knot number and the prior on the weight controls?

Suppose \(D_{i}\) be the date of year of the cherry blossom in year \(i\) then a formal description of the model is:

\[D_{i} \sim N(\mu_{i},\sigma)\] \[\mu_{i} = \alpha + \sum_{k=1}^{K}w_{k}B_{ki}\] \[\alpha \sim N(100,10)\] \[w_{k} \sim \text{Normal}(0,10)\] \[\sigma \sim \text{Exponential}(1)\]

\(B_{ki}\) is the value of the \(k\)-th basis function for year \(i\).

url = 'https://raw.githubusercontent.com/rmcelreath/rethinking/'\
'master/data/cherry_blossoms.csv'
d = pd.read_csv(url, sep=';', header=0)
d.head()
year doy temp temp_upper temp_lower
0 801 NaN NaN NaN NaN
1 802 NaN NaN NaN NaN
2 803 NaN NaN NaN NaN
3 804 NaN NaN NaN NaN
4 805 NaN NaN NaN NaN 
d2 = d.dropna(subset=['doy'])
d2.head()
year doy temp temp_upper temp_lower
11 812 92.0 NaN NaN NaN
14 815 105.0 NaN NaN NaN
30 831 96.0 NaN NaN NaN
50 851 108.0 7.38 12.1 2.66
52 853 104.0 NaN NaN NaN 
num_knots = 15
knot_list = np.quantile(d2.year, np.linspace(0, 1, num_knots))
Code 
knot_list
array([ 812., 1036., 1174., 1269., 1377., 1454., 1518., 1583., 1650.,
       1714., 1774., 1833., 1893., 1956., 2015.])
B = dmatrix(
    "bs(year, knots=knots, degree=3, include_intercept=True) - 1",
    {"year": d2.year.values, "knots": knot_list[1:-1]},
)
Code 
np.asarray( B ).shape
(827, 17)
Code 
B
DesignMatrix with shape (827, 17)
  Columns:
    ['bs(year, knots=knots, degree=3, include_intercept=True)[0]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[1]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[2]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[3]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[4]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[5]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[6]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[7]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[8]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[9]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[10]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[11]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[12]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[13]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[14]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[15]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[16]']
  Terms:
    'bs(year, knots=knots, degree=3, include_intercept=True)' (columns 0:17)
  (to view full data, use np.asarray(this_obj))

Let’s plot the basis functions.

Code 
_, ax = plt.subplots(1, 1, figsize=(12, 4))
for i in range( B.shape[1] ):
    ax.plot(d2.year, (B[:, i]))
ax.set_xlabel("year")
ax.set_ylabel("basis");

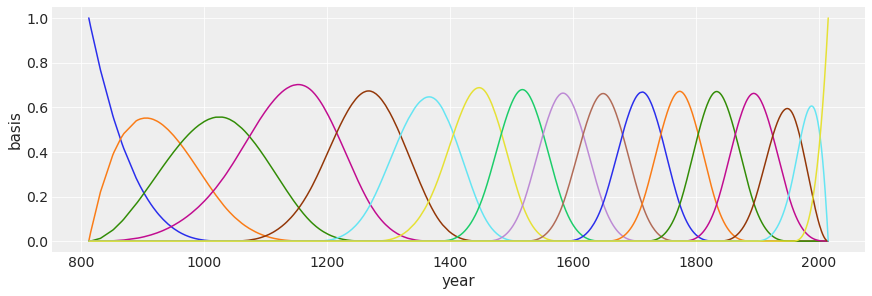
Next, let’s learn the parameters.

with pm.Model() as m_4M8:
    a = pm.Normal("a", 100, 10)
    w = pm.Normal("w", mu=0, sd=10, shape=B.shape[1])
    mu = pm.Deterministic("mu", a + pm.math.dot(B.base, w.T))
    sigma = pm.Exponential("sigma", 1)
    D = pm.Normal("D", mu, sigma, observed=d2.doy)
    trace_m_4M8 = pm.sample(2000, tune=2000, chains=2, 
                            return_inferencedata=False)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Sequential sampling (2 chains in 1 job)
NUTS: [sigma, w, a]
Sampling 2 chains for 2_000 tune and 2_000 draw iterations (4_000 + 4_000 draws total) took 81 seconds.
The number of effective samples is smaller than 25% for some parameters.
100.00% [4000/4000 00:40<00:00 Sampling chain 0, 0 divergences]
100.00% [4000/4000 00:40<00:00 Sampling chain 1, 0 divergences]

Plot each basis weighted by it’s corresponding parameter.

Code 
_, ax = plt.subplots(1, 1, figsize=(12, 4))
wp = trace_m_4M8['w'].mean(0) #17 entries, one for each basis fn
for i in range( B.shape[1] ):
    ax.plot(d2.year, (wp[i] * B[:, i]), color="C0")
ax.set_xlim(812, 2015)
ax.set_ylim(-6, 6);

post_pred = ( az.summary(trace_m_4M8, var_names=["mu"], hdi_prob=0.94).
             reset_index(drop=True) )
post_pred.head()
Got error No model on context stack. trying to find log_likelihood in translation.
/usr/local/lib/python3.7/dist-packages/arviz/data/io_pymc3_3x.py:102: FutureWarning: Using `from_pymc3` without the model will be deprecated in a future release. Not using the model will return less accurate and less useful results. Make sure you use the model argument or call from_pymc3 within a model context.
  FutureWarning,
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
0 100.320 3.179 93.831 105.847 0.050 0.035 4039.0 3348.0 1.0
1 100.406 2.994 94.330 105.655 0.047 0.033 4124.0 3292.0 1.0
2 100.822 2.182 96.796 105.020 0.032 0.023 4692.0 3168.0 1.0
3 101.262 1.555 98.286 104.116 0.021 0.015 5426.0 3262.0 1.0
4 101.302 1.514 98.484 104.162 0.021 0.015 5442.0 3287.0 1.0 
plt.fill_between(
    d2.year,
    post_pred["hdi_3%"],
    post_pred["hdi_97%"],
    color="firebrick",
    alpha=0.4,
);

ax = plt.gca()
ax.plot(d2.year, d2.doy, "o", alpha=0.3)
for knot in knot_list:
    ax.axvline(knot, color="grey", alpha=0.4);
ax.plot(d2.year, 
        post_pred['mean'],
        lw=3, color="firebrick")

fig = plt.gcf()
fig.set_size_inches(12, 4)
ax.set_xlabel("year")
ax.set_ylabel("days in year")
ax.set_title(f'knots={num_knots}')
Text(0.5, 1.0, 'knots=15')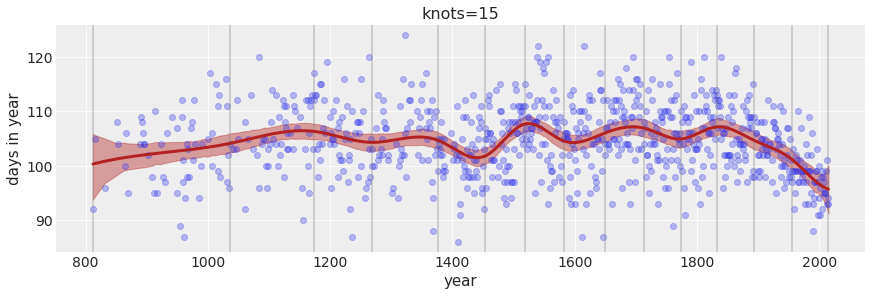

Increase the number of knots to 30.

Text(0.5, 1.0, 'knots=30')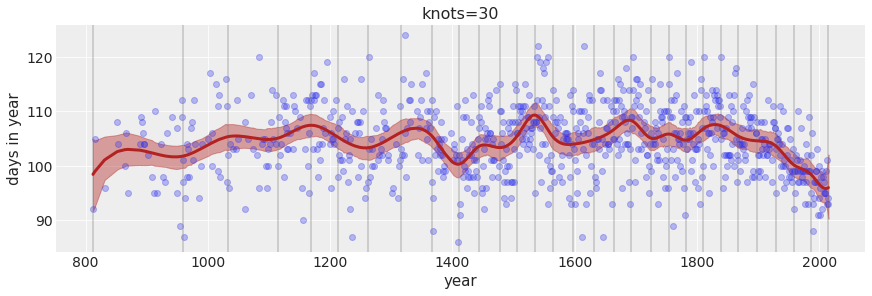

Change the width of the prior on the weights.

Text(0.5, 1.0, 'knots=30; w ~ N(0,100)')

Text(0.5, 1.0, 'knots=30; w ~ N(0,1)')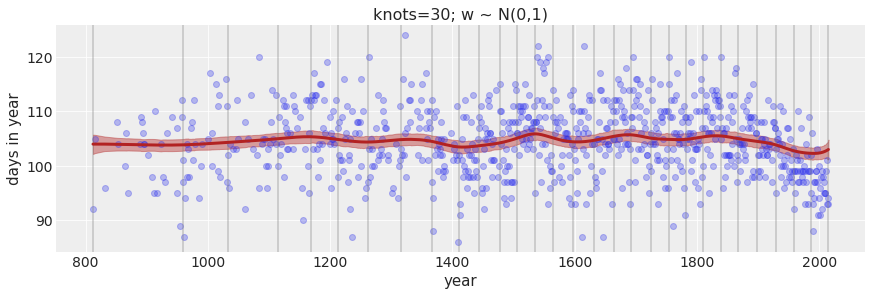

Text(0.5, 1.0, 'knots=5; w ~ N(0,100)')

The larger the number of knots the more local variation we are able to capture. The prior on the weight controls how much weights are allowed to vary around the mean. A tighter (smaller) standard deviation on the weight will not allow the weight to vary much.

References

[1]
Wikipedia, “<A href="http://en.wikipedia.org/w/index.php?title=log-normal%20distribution&oldid=1080654936">"Log-normal distribution — Wikipedia, the free encyclopedia"</a>.” http://en.wikipedia.org/w/index.php?title=Log-normal%20distribution&oldid=1080654936, 2022.